气化炉是煤、生物质等进行气化生产合成气的核心装置，气化反应主要在气化炉燃烧室内进行，燃烧室内层由高温耐火砖构成。因燃烧室内工作温度通常达1300℃以上，且长期受酸性气体冲蚀，以及高温高压冲击，耐火砖在气化炉运行过程中逐渐退化，甚至破损，危及整个气化炉的性能和运行安全。为保证气化炉的运行安全，为其制定合理的维护策略非常重要，而且视情维修(CBM)能在很大程度上降低维修风险和成本并保证气化炉的可靠性，准确的剩余寿命预测可为CBM提供可靠依据，这对保障气化炉的正常性能和运行安全意义重大。

　　为提高耐火砖使用寿命，近年来众多研究人员从改进耐火砖加工材料及工艺、改善耐火砖性能、预测耐火砖热面温度和剩余厚度等方面进行了大量研究。在改进加工材料及工艺来提高耐火砖使用寿命方面，HASSAN等考察了掺入粉煤灰生产耐火砖对其性能的影响，结果证明掺入粉煤灰可以提高耐火砖的耐热性。类似的，DAL等研究发现添加轻质硅藻土生产耐火砖同样可以改善耐火砖性能。RAMEZANI等考察了发泡聚苯乙烯造孔剂的粒径对耐火砖导热性的影响。GARCIA-PRIETO等考察了显微组织特征对耐火砖性能和断裂韧性的影响，并建立了耐火材料微观结构和织构及其韧性之间的基本关系。在改善耐火砖性能来提高耐火砖使用寿命方面，CHEN等考察了耐火砖的腐蚀机理和影响因素并提出了抑制腐蚀的措施。ZOU等考察了具有微/纳米孔的轻质镁质耐火砖在静磁场作用下的抗渣侵蚀性能，结果表明在8.5mT的静磁场下，它们表现出优异的抗渣性。除此之外，EL-LEATHY等考察了在高效减水剂存在下耐火砖基砂浆的热性能，并给出了提高耐火砖的耐热性的建议和措施。前人还对耐火砖的物理力学热性、热冲击特性和电阻加热能量储存性能开展了研究。在预测耐火砖的热面温度和剩余厚度方面，ZHANG等预测了耐火砖组成的内轮廓的热面温度。DMITRIEV等开发了高炉炉缸耐火砖内衬侵蚀监控系统，实现了根据温度变化对耐火砖的剩余厚度进行预测。但其仅对耐火砖的剩余厚度进行了预测，没有进一步对耐火砖的当前状态和剩余寿命进行诊断和预测，无法为耐火砖维护策略的制定提供有效的依据和建议。

　　尽管当前为改善耐火砖性能和提高其使用寿命，学者从加工材料、加工工艺和性能等方面开展了大量研究，但对耐火砖健康状态诊断和剩余寿命预测的研究却鲜有报道。赵嘉煜等对增压锅炉耐火砖疲劳裂纹扩展特性进行了研究，得出了裂纹尺寸与应力强度因子的关系曲线，并预估了耐火砖剩余寿命。但根据裂纹扩展速率建立的剩余寿命计算公式只针对存在裂纹缺陷的耐火砖，且只能粗略估算出耐火砖还能承受的锅炉开停车的剩余次数，不能对耐火砖的剩余寿命进行准确预测。LUOY等研究了多孔耐火材料的抗热震性，并用应变寿命疲劳法预测了多孔耐火材料的热冲击循环次数，并指出其能承受外部载荷的最大疲劳寿命。但没有基于耐火砖的历史剩余寿命数据实现耐火砖整个退化过程中剩余寿命的实时预测。

　　笔者聚焦于耐火砖的健康状态诊断和剩余寿命预测，为了提高诊断的科学性和预测的准确性，首次构建了基于隐半马尔可夫模型(HSMM)的气化炉耐火砖健康状态诊断和剩余寿命预测模型。HSMM是在隐马尔可夫模型(HMM)的基础上发展而来的，弥补了HMM的“马尔可夫局限性”,能很好地还原状态转变路径，在HMM的基础上加入了状态驻留时间分布，比HMM更符合实际退化规律，从而可以直接准确地进行剩余寿命预测。目前，许多研究人员用HSMM建立退化模型进行故障诊断和剩余寿命预测。在故障诊断方面，采用HSMM对磁盘故障、电机磨损程度、裂纹扩展和设备退化过程等进行了故障诊断和预测研究。其中，FANL等基于HSMM对疲劳裂纹进行了故障诊断和预测，并与HMM进行了对比，验证了HSMM的有效性和优越性。在健康状态诊断方面，将HSMM应用到机械设备以及其他设备的健康状态诊断的研究中。其中，LIUT等用HSMM对铣削过程刀具磨损状态进行了估计和在线监测。在剩余寿命预测方面，人们提出了许多基于HSMM的剩余寿命预测方法，并对各种设备的剩余寿命进行了预测研究。比如：MAY等提出了一种基于稀疏表示特征和隐半马尔可夫模型的剩余寿命预测方法。虽然目前已有较多关于HSMM用作诊断和预测的研究，但研究对象多为轴承、齿轮、电机和其他机械领域的设备，在以往文献中对气化炉耐火砖的研究鲜有报道。

　　笔者对某公司气化炉燃烧室耐火砖进行了健康状态诊断和剩余寿命预测研究。研究过程基于燃烧室耐火砖在实际工况下有效厚度的测量数据进行。基于各状态的训练数据为耐火砖构建了健康状态诊断模型，包含耐火砖各状态对应的模型;还基于耐火砖的全寿命周期数据构建了寿命预测模型，包含了耐火砖的全部状态。基于以上2种模型对耐火砖的当前状态进行了诊断，并预测了其剩余寿命。最终对比分析和讨论了所得结果，总结了气化炉耐火砖的退化规律，还为耐火砖的维护策略提供了建议。

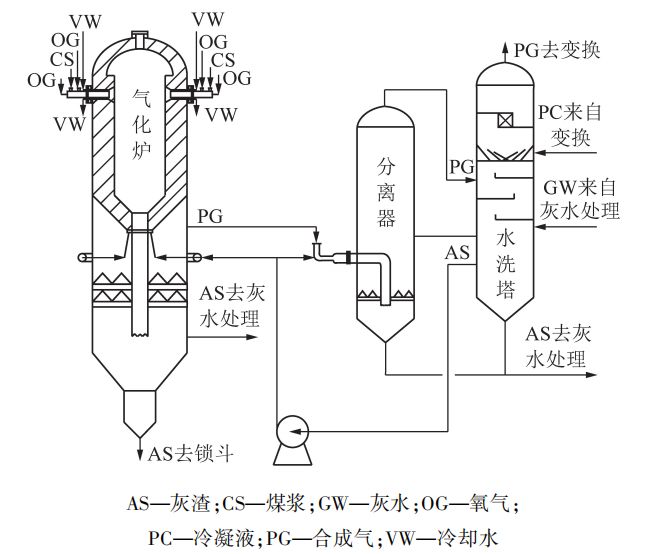
　　水煤浆气化是该公司的关键工序，为后续的尿素、甲胺、甲醛、DMF、醋酸、多元醇、己二酸、乙二醇、三胺、复合肥等各产品车间提供原料气。该公司目前拥有大氮肥气化平台、工业园东区气化平台和工业园北区气化平台三大气化平台，拥有3台四喷嘴和9台顶喷式水煤浆气化炉，煤炭消耗量约450万t/a。水煤浆气化工艺流程如图1所示。

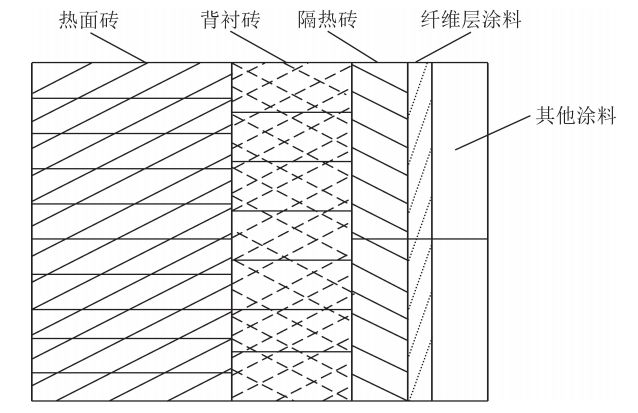
　　(1)热面砖。一般用于保护燃烧室隔热层免受熔融状态下的炉渣侵蚀，多为致密铬铝锆异型砖。

　　(4)纤维涂抹料。一般用于缓冲内层耐火砖受热膨胀对燃烧室外壳的冲击力，为外壳隔绝高温。

　　该公司气化炉燃烧室内部高温耐火层的热面砖由50层耐火砖砌成。为了保证气化炉的安全运行，该公司制定的耐火砖最小剩余量指标为50mm,原始厚度为228mm。

　　在水煤浆气化炉正常运作期间，由于燃烧室内水煤浆和氧气不完全氧化反应的发生，耐火砖需要承受高温高压冲击、合成气的冲刷、熔融状态炉渣的侵蚀和磨损。所以随着水煤浆气化炉的运行，耐火砖会受到不良冲击而逐渐退化。而造成耐火砖退化的原因主要包括：

　　(1)高温烧蚀。水煤浆煤的灰分具有较高的熔点，这决定了水煤浆气化炉的操作温度需要保持在1300℃以上。而在水煤浆气化炉运行期间，处于向火面的耐火砖直接承受如此高的温度，长此以往就会对耐火砖造成一定的烧蚀损坏。

　　(2)气流冲刷。水煤浆气化炉燃烧室内部的气流具有较高的速度，并裹挟着炉渣对耐火砖进行一定的冲蚀和摩擦，同样会造成耐火砖的退化。

　　(3)熔融状态炉渣磨损和侵蚀。水煤浆和氧气发生不完全氧化反应会产生高速流动的熔融状态炉渣，会冲刷耐火砖并造成一定的磨损。炉渣还会进入耐火砖的孔隙之中，造成耐火砖孔隙的膨胀。

　　(4)化学侵蚀。在气化炉燃烧室内的高温作用下，熔渣中的CaO,Fe₂O₃等会和耐火砖中的金属氧化物形成化合物进入耐火砖内部，造成耐火砖的损坏。

　　(5)热应力冲击。水煤浆气化炉开停车会产生很大的温度波动，从而产生作用于耐火砖的热应力。

　　(6)沉积碳的膨胀应力。气化炉燃烧室中的还原性气体H₂和CO会进入耐火砖孔隙之中并与耐火砖中的氧化物发生反应，造成碳的沉积，由于碳和耐火砖的热膨胀系数不同，所以会造成耐火砖的退化。

　　隐半马尔可夫模型(HSMM)在隐马尔可夫模型(HMM)基础上发展而来，并弥补了HMM的“马尔可夫局限性”,其拓扑结构如图3所示，其宏观状态属于马尔可夫过程，但微观状态不属于马尔可夫过程，所以被称为隐“半”马尔可夫模型。

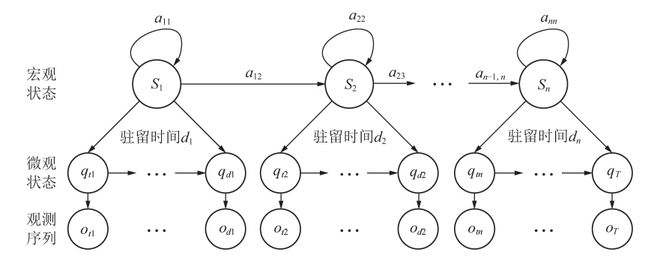
　　(3)初始状态概率分布：π。初始状态概率分布π={π,π2,…,π N },表示初始阶段处于各个状态的概率分布。

　　(4)状态转移概率矩阵：A={a ij },其中，aij为从状态i转移到状态j的概率，1≤i，j≤N。

　　(5)观测值概率矩阵：B= ,其中bi(Ot)为在状态i中，观测值为Ot,的概率，1≤i≤N,1≤t≤M。

　　(6)状态驻留时间概率矩阵：P= 。其中Pi(d)为状态i的驻留时间为d的概率。

　　因此N个状态，M个观测值的HSMM可以简化表示为：λ=(π,A,B,P),λ为HSMM模型的简化表达。

　　由于HSMM对HMM进行了改进，解决HSMM面临问题的算法也都进行了改进，它们分别为改进的Forward算法、改进的Baum-Welch算法、改进的Viterbi算法，分别用于解决HSMM在实际应用中面临的评估问题、学习问题、解码问题。

　　改进的Forward算法用于解决HSMM在实际应用中面临的评估问题，即在给定观测序列0以及模型λ的条件下，计算λ产生0的概率P(O│A)。

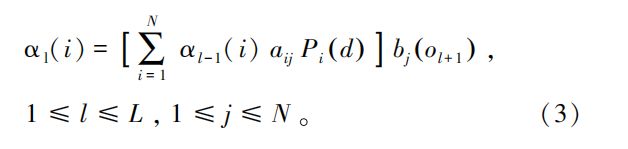
　　改进的Baum-Welch算法用于解决HSMM在实际应用中面临的学习问题，即在给定观测序列0的前提下，确定使λ产生0的概率P(O│λ)最大的模型参数。也就是重新估计模型参数π₀,A₀,B₀,P₀使得λ产生O的概率P(O│λ)最大。采用改进的Baum-Welch算法对模型参数进行重新估计，直到模型产生的概率最大，输出此时重新估计后的参数，这个过程也就是HSMM的训练过程。

　　HSMM引入了状态驻留时间概率矩阵P,假设它服从高斯分布。具体流程如下：

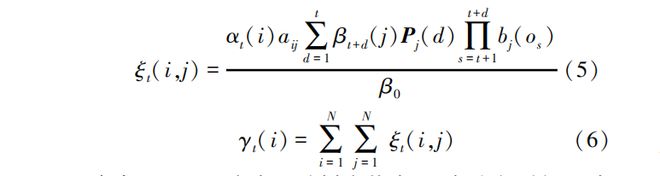
　　式中，ξ,(i,j)为在t时刻为状态i,在驻留时间d内由状态i转变为状态j的概率;γ,(i)为已知观测值序列，t时刻处于状态i的概率。

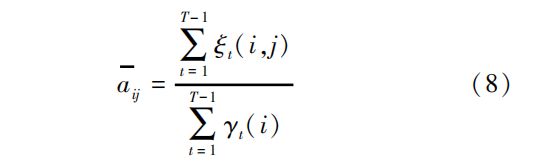
　　式中，G为高斯分量的个数;H为观测概率的均值;U为观测概率的方差;w为观测概率的权值。

　　改进的Viterbi算法用于解决HSMM在实际应用中面临的解码问题，即在给定观测序列0以及模型λ的条件下，确定0对应的最优状态序列S*。

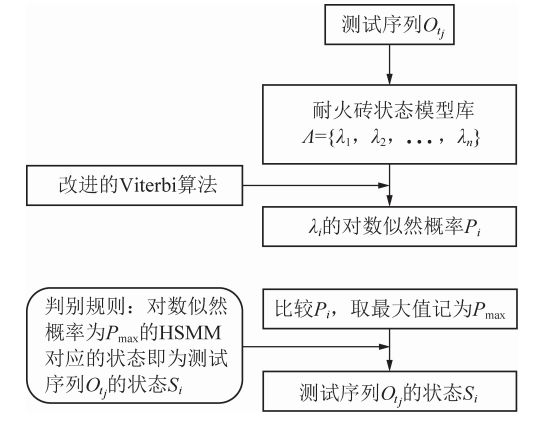
　　耐火砖健康状态诊断和剩余寿命预测模型的建模流程如图4所示，主要包括模型训练、健康状态诊断和剩余寿命预测三大部分。

　　(1)模型训练。需要为气化炉耐火砖建立一个状态模型库和一个全寿命周期模型。

　　首先，按照图5中的训练步骤为耐火砖建立一个状态模型库，即为耐火砖的n个状态建立并训练对应的HSMM,分别为：HSMM,,HSMM₂,…,HSMM,将状态模型库定义为A={λ₁,λ₂,…,λn},从而可以通过不同的HSMM描述耐火砖不同的状态。

　　然后，用改进的Baum-Welch算法根据耐火砖全寿命周期的训练数据建立并训练一个全寿命周期模型HSMM,,包含耐火砖的所有状态，可以描述耐火砖在整个寿命周期内在不同状态之间的转变和驻留。

　　(2)健康状态诊断。耐火砖健康状态诊断流程如图6所示，总体步骤为，首先用改进的Viterbi算法计算测试序列0,和耐火砖状态模型库A中各状态模型λ的对数似然概率P₁;然后比较P,的大小，取最大值记为Pm;最后，判断状态模型库A中哪个HSMM和测试序列0,产生了最大对数似然概率Pmax,该HSMM对应的状态Si即为测试序列Otj的状态Si，也就实现了耐火砖的健康状态诊断。

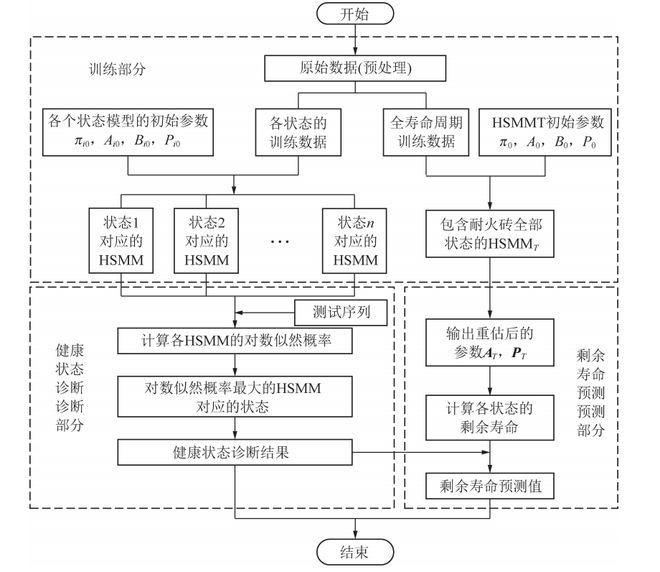
　　(3)剩余寿命预测。根据训练HSMM,得到的重估参数：状态转移概率矩阵A,和状态驻留时间概率矩阵P,,并在其基础上计算各状态驻留时间的均值μ和方差σ²,接着计算耐火砖各状态的最大驻留时间D。,再结合重估参数A,计算耐火砖各状态的剩余寿命RUL,最后根据测试序列0,的健康状态诊断结果预测其剩余寿命。

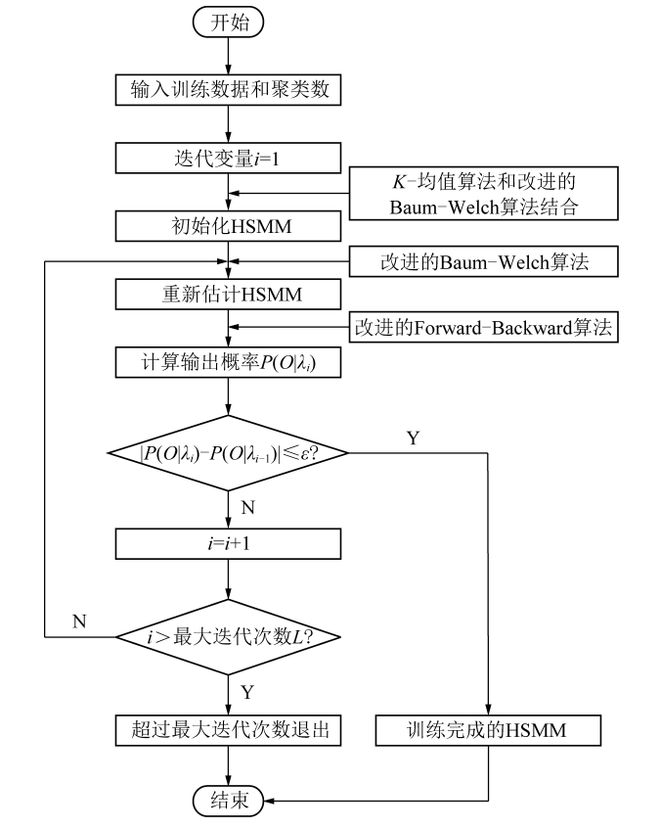
　　本节对该公司气化炉燃烧室实际工况下的内衬耐火砖进行了健康状态诊断和剩余寿命预测。该公司气化炉燃烧室内衬高温耐火层由从下到上共50层耐火砖构成。表1记录了从第1天到第780天，相同观测时间间隔内，这50层耐火砖在正常工况下有效厚度的测量数据。随着观测时间的延长，各层耐火砖的有效厚度逐渐减少，由此可见耐火砖会随着气化炉的运行逐渐退化直至损坏。由于过于频繁的开停车会对气化炉的正常运行造成不良影响，从而无法保证在正常工况下测量气化炉耐火砖的有效厚度，并影响耐火砖全寿命周期数据的准确性。所以本文的研究数据是以相等的时间间隔对气化炉耐火砖的有效厚度进行测量，并在此基础上对耐火砖的全寿命周期数据进行拟合处理，为后续的模型训练获得大量的训练数据，从而在保证准确测量正常工况下气化炉耐火砖的有效厚度的前提下，实现耐火砖健康状态诊断和剩余寿命预测模型训练数据以及测试序列的获取。对表1中的数据进行曲线拟合处理，并用K-均值聚类算法对取得的拟合数据进行聚类处理，根据得到的聚类中心并结合耐火砖的实际退化情况，将气化炉耐火砖的退化过程划分为4个状态，分别为：S₁(正常退化),S₂(轻微退化),S₃(加速退化)和S₄(严重退化)。并对耐火砖健康状态诊断和剩余寿命预测模型的训练数据以及测试序列进行标准化处理，以便于后续模型的训练。标准化规则由K-均值聚类结果制定，见表2。

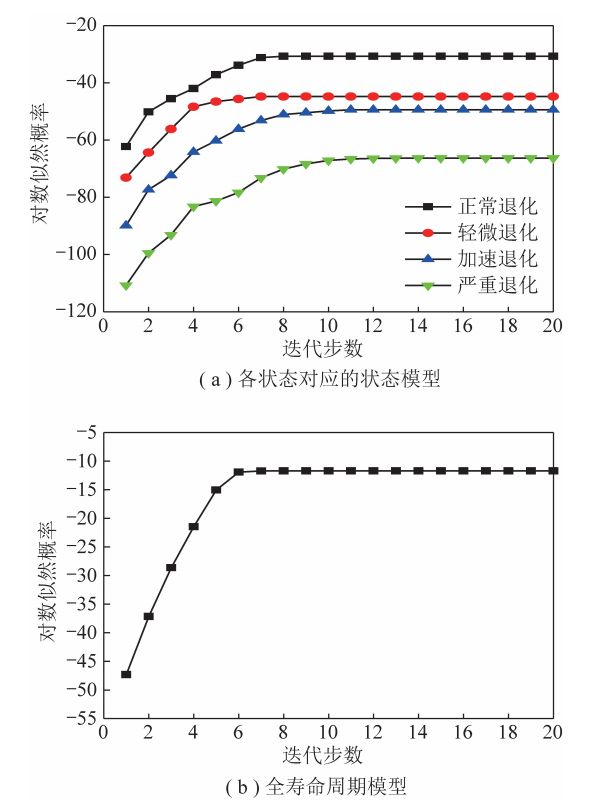
　　4个状态对应的状态模型和全寿命周期模型的训练过程如图7所示。其中，设定最大迭代步数为20,收敛误差e=0.0001。图7(a)为耐火砖各状态对应的状态模型的训练过程，图7(b)为全寿命周期模型的训练过程。随着训练次数的增加，各模型的对数似然概率也逐渐增加，直到达到收敛条件不再增加，也就意味着模型收敛，训练完成。各状态模型和全寿命周期模型都在20次训练以内就达到收敛，说明所构建的模型具有良好的学习能力。

　　在气化炉耐火砖状态模型库构建完成后，将处于S₁(正常退化),S₂(轻微退化),S₃(加速退化)和S₄(严重退化)的各10个测试序列输入其中，计算它们和各状态模型的对数似然概率，结果如图8所示，其中，图8(a),(b)分别为S₁~S₄的测试序列和气化炉耐火砖状态模型库中各状态模型的对数似然概率。在图8(a)中，可以看出测试序列和正常退化模型的对数似然概率始终处于最上方，符合测试序列的实际状态。在图8(b)中，除5号测试序列和轻微退化模型的对数似然概率不是最大外，其余均为最大。在图8(c)中，可以看出测试序列和加速退化模型的对数似然概率始终最大，符合测试序列的实际状态。在图8(d)中，仅有7号测试序列和严重退化模型的对数似然概率不是最大，其余均为最大。

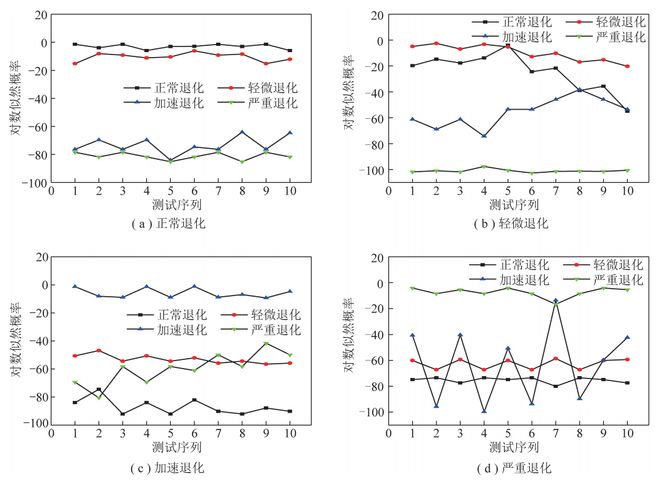
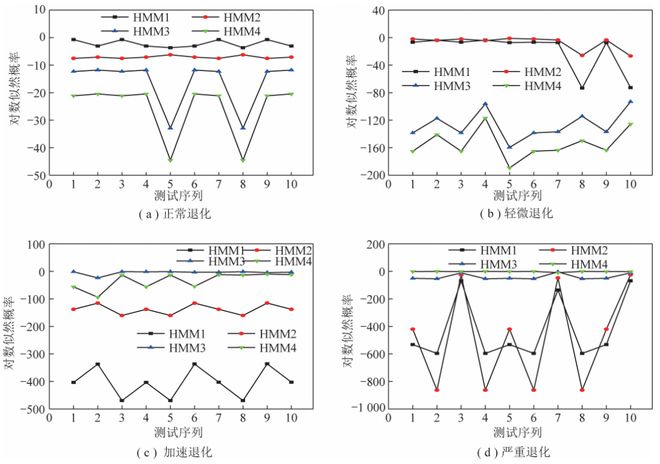
　　图9是各状态的测试序列和不同状态对应的HMM的对数似然概率。在图9(a)中，测试序列和HMM₁的对数似然概率始终处于最上方，符合测试序列的实际状态。在图9(b)中，在10个测试序列和HMM₂的对数似然概率中，2号和4号测试序列不是最大，这里HMM错将实际状态为轻微退化的2号和4号测试序列错误诊断为正常退化。在图9(c)中，测试序列和HMM3的对数似然概率始终最大，符合测试序列的实际状态。在图9(d)中，除7号测试序列外，其他9个测试序列和HMM₄的对数似然概率都是最大值，这里HMM错将实际状态为严重退化的7号测试序列诊断为加速退化。

　　对比图8,9可以发现，部分测试序列和各HMM的对数似然概率发生了重叠，不利于判断耐火砖的当前状态，而测试序列和各HSMM的对数似然概率区分比较明显，相较于HMM不易发生“误诊”现象。

　　采用基于HSMM构建的气化炉耐火砖健康状态诊断模型得到的各状态的测试序列的健康状态诊断结果见表3。对正常退化和加速退化的测试序列进行健康状态诊断的正确率均为100%,而对轻微退化和严重退化的测试序列进行健康状态诊断的正确率为90%,这可能是由于在用K-均值聚类算法对原始数据进行特征提取时，正常退化和轻微退化的原始数据以及加速退化和严重退化的原始数据发生了一定的重叠，导致极个别轻微退化的测试序列和正常退化模型相似度较高以及严重退化的测试序列与加速退化模型的相似度较高。

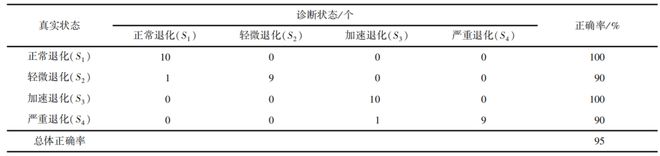
　　表4是基于HMM对耐火砖进行健康状态诊断的结果，对正常退化和加速退化的测试序列进行健康状态诊断的正确率均为100%,而对轻微退化的测试序列进行健康状态诊断的正确率为80%,对严重退化的测试序列进行健康状态诊断的正确率为90%。

　　对比表3,4可以发现基于HMM和HSMM对耐火砖进行健康状态诊断的效果差别不大，基于HSMM取得的效果稍好，总体正确率为95.0%,大于HMM的总体正确率92.5%。这是因为HSMM在HMM基础上加入的状态驻留时间概率矩阵P对其健康状态诊断性能影响较小，所以基于二者对耐火砖进行健康状态诊断的效果也相差不大。

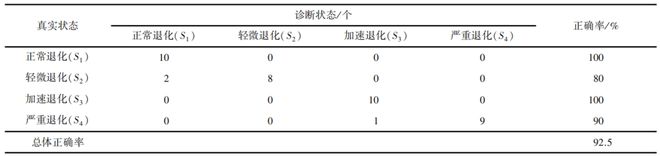
　　图10为基于HMM和HSMM得到的相等时间间隔的44个测试序列的健康状态诊断结果。这44个测试序列由4组数据组成，第1组为观测时间0~120d,第1层到第50层耐火砖的测试序列;第2组为观测时间220~340d,第1层到第50层耐火砖的测试序列;第3组为观测时间440~560d,第1层到第50层耐火砖的测试序列;第2组为观测时间660~780d,第1层到第50层耐火砖的测试序列。

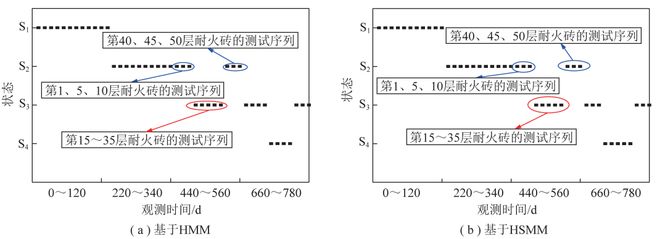
　　在图10(a)中，在44个分别处于耐火砖各寿命阶段的测试序列中，处于严重退化(S₄)的最少，仅有4个，而处于轻微退化(S₂)的最多，有16个，处于正常退化(S₁)和加速退化(S₃)的均为12个。在图9(b)中，处于严重退化(S₄)的最少，仅有5个，而处于轻微退化(S₂)的最多，有17个，处于正常退化(S₁)和加速退化(S₃)的均为11个。由此可以推断在整个寿命周期内，耐火砖在轻微退化(S₂)的持续时间最长，在严重退化(S₄)的持续时间最短，在正常退化(S₁)和加速退化(S₃)的持续时间相差不多。

　　也从侧面说明了耐火砖在轻微退化(S₂)退化速度较慢，而在严重退化(S₄)则加快退化速度，很快就会到达损坏状态。

　　而且在同一观测时间440~560d内，蓝色圆圈圈住部分是第1,5,10层和第40,45,50层耐火砖的测试序列，它们的状态为轻微退化(S₂)。而红色圆圈圈住部分是第15~35层耐火砖的测试序列，它们的状态为加速退化(S₃)。在观测时间660~780d中也出现了同样的现象，这说明气化炉燃烧室中间位置的第15~35层耐火砖的退化程度相对其他位置的耐火砖是比较严重的，而处于燃烧室上方和下方的耐火砖退化程度较低。而在观测时间0~120d和220~340d内不同位置耐火砖的状态是一致的，这也说明了不同部位耐火砖在其寿命前期的退化程度相差不大，而随着气化炉的运行，处于燃烧室中间位置的耐火砖的退化速度不断加快，导致了退化程度的加深，以至于在耐火砖寿命后期表现出比其他位置耐火砖更为严重的退化情况。

　　以上结论可以为合理制定耐火砖的维护策略提供一定的建议：处于燃烧室不同位置的耐火砖退化速度不一样，所以需要区别对待，分别为不同部位的耐火砖制定合理的维护策略。譬如，处于燃烧室中间位置的耐火砖退化更快，这需要更短周期的定期检查与维护，而处于燃烧室上方和下方的耐火砖退化较慢，则可以进行较长周期的检查与维护。同样，不仅不同部位的耐火砖的退化速度不一样，在其寿命周期不同时段的耐火砖的退化速度也不一样。在耐火砖的寿命前期，其退化速度较为缓慢，没有必要进行过于频繁的检查和维护，从而浪费人力物力。但在耐火砖的寿命后期，尤其是在严重退化(S₄),由于其退化速度较快，需要频繁并及时对其进行检查和维护或考虑对其进行更换，以保证气化炉的运行安全和正常性能。

　　由于气化炉燃烧室不同位置耐火砖的退化速度和退化程度不一致，导致它们的剩余寿命长短不一，本文以退化最严重的第25层耐火砖为例，采用基于HSMM构建的气化炉耐火砖寿命预测模型对各状态的剩余寿命进行预测。

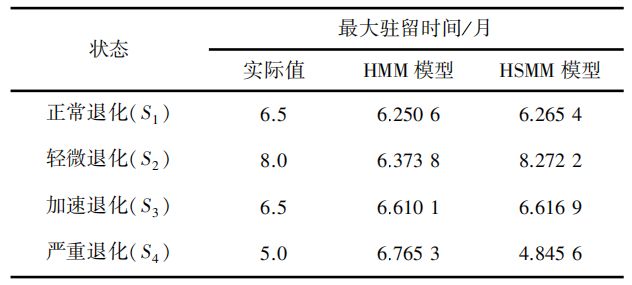
　　首先，根据训练气化炉耐火砖全寿命周期模型得到的重估参数计算各状态驻留时间的均值和方差，在此基础上，采用式(18)计算气化炉耐火砖各状态的最大驻留时间，并与基于HMM得到的结果进行了对比，结果见表5。基于HMM得到的耐火砖各状态的最大驻留时间几乎相等，和实际值有一定出入。而基于HSMM得到的耐火砖各状态的最大驻留时间与实际值具有相同的变化趋势。这是因为基于HMM对耐火砖进行剩余寿命预测时具有一定的“马尔可夫局限性”,它根据重估后的状态转移概率矩阵定义的状态驻留时间概率矩阵不符合耐火砖的实际退化规律，所以无法较好地描述耐火砖的退化过程。而HSMM的状态驻留时间概率矩阵是根据耐火砖的全寿命周期数据训练得到的，比较符合耐火砖的实际 退化规律，能较好还原耐火砖退化过程中不同状态的转换路径和驻留时间。

　　以表5中气化炉耐火砖各状态的最大驻留时间为基础，结合全寿命周期模型的重估参数：状态转移矩阵A,,按照式(19)~(21)计算气化炉耐火砖各状态的剩余寿命，结果见表6。基于HSMM得到的各状态剩余寿命预测值全部落在耐火砖各状态实际寿命的区间内，说明预测效果良好、较为准确。预测正确率是用预测值和各状态实际剩余寿命的均值计算所得。其中，正常退化的剩余寿命预测正确率较高，达到了99.71%;轻微退化的剩余寿命预测正确率也达到了87.81%;但加速退化和严重退化的剩余寿命预测正确率较低，仅为79.02%和58.89%。这可能是因为气化炉耐火砖全寿命周期模型的参数：状态驻留时间概率矩阵的定义与气化炉耐火砖的实际退化情况有些偏差，导致加速退化和严重退化2种状态的剩余寿命预测值不太理想。但基于该模型对气化炉耐火砖各状态的剩余寿命进行预测的总体正确率达到了81.36%,得到了较为准确的结果。

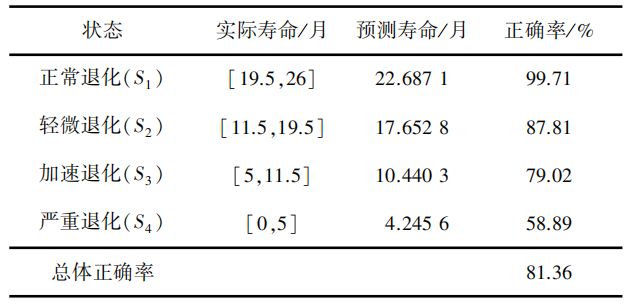
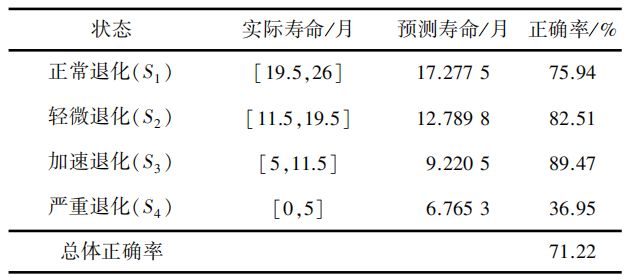
　　表7是基于HMM预测的耐火砖各状态的剩余寿命和实际值的对比。由表7可知，HMM得到的正常退化和严重退化的剩余寿命预测值都没有落入实际剩余寿命区间内，导致基于HMM对耐火砖进行剩余寿命预测的正确率较低，总体正确率只有71.22%。考虑是由于HMM获得的耐火砖各状态的最大驻留时间不符合耐火砖实际退化规律导致的。

　　基于HSMM得到的各状态的最大驻留时间预测值和剩余寿命预测值与基于HMM得到的预测值及实际值的对比如图11所示。其中，实际剩余寿命不考虑在气化炉运行过程中短暂停车以及检修的影响，只考虑耐火砖随着气化炉的运行逐渐退化的过程，因此表现为一条随着运行时间增加而逐渐减少的直线 耐火砖各状态最大驻留时间预测值和剩余寿命预测值与实际值的对比

　　在图11(a)中可以发现，基于HSMM预测的耐火砖各状态的最大驻留时间与实际最大驻留时间具有相同的趋势，虽然最大驻留时间预测值与实际值存在一定的误差，但是相差不大，而且整体趋势相符。但基于HMM得到的预测值和实际值的趋势完全不一致，这是因为HMM定义的耐火砖状态驻留时间概率矩阵不符合其实际退化规律，不能很好描述耐火砖的退化过程，所以HSMM比HMM更适合对耐火砖进行剩余寿命预测。这也说明所建立的气化炉耐火砖剩余寿命预测模型符合耐火砖的实际退化规律。由图11(b)可以发现，基于HSMM的气化炉耐火砖剩余寿

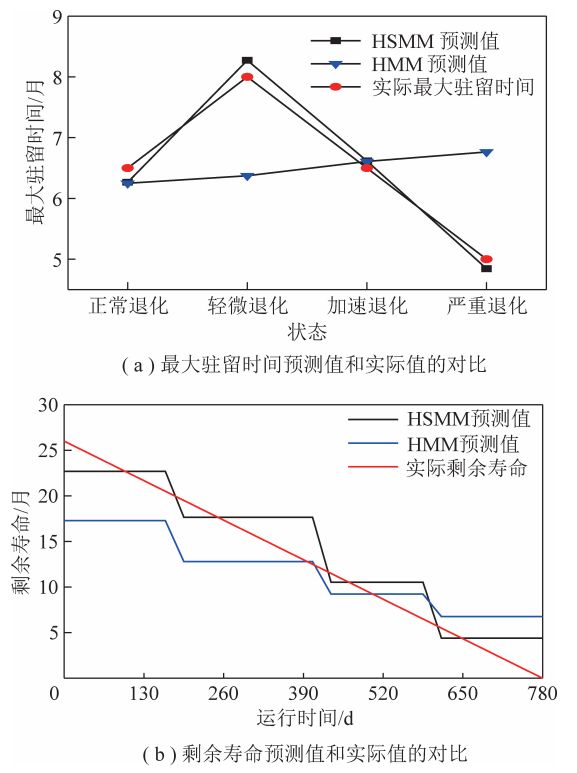
　　命预测模型得到的耐火砖各状态的剩余寿命预测值与实际值基本符合，全都落在了实际剩余寿命区间内，但基于HMM得到的剩余寿命预测值却与实际值相差甚远，仅在运行时间390~650d内与实际值相符，其余预测值均没有落到实际剩余寿命区间内，预测准确性较差。这也说明所建立的气化炉耐火砖剩余寿命模型能较好地预测气化炉耐火砖的剩余寿命。

　　(1)建立了气化炉耐火砖的健康状态诊断模型和剩余寿命预测模型，并基于此对耐火砖进行健康状态诊断和剩余寿命预测。其结果可为合理制定耐火砖的维护策略提供建设性建议，也为实际生产中制定气化炉耐火砖维护策略提供了新的思路和解决方案。

　　(2)对实际气化炉耐火砖开展工程应用，对耐火砖的40个测试序列进行健康状态诊断，诊断正确率达到95%,大于基于HMM的诊断正确率92.5%,取得了良好的诊断效果。分析了同一时间不同位置耐火砖的健康状态诊断结果，发现处于燃烧室中间位置的耐火砖比上层和下层的耐火砖退化更快、更严重;不同部位耐火砖在其寿命前期的退化程度相差不大，随着气化炉的运行，处于燃烧室中间位置的耐火砖的退化速度不断加快，导致了退化程度的加深。分析了同一位置的耐火砖在不同寿命阶段的健康诊断结果，发现耐火砖在轻微退化持续时间最长，正常退化和加速退化持续时间稍短，严重退化持续时间最短。(3)对气化炉燃烧室第25层耐火砖进行剩余寿命预测，基于HSMM各状态的剩余寿命预测值全部落入实际剩余寿命区间内，平均准确率达到了81.36%,大于基于HMM的平均准确率71.22%。这表明基于HSMM构建的耐火砖寿命预测模型取得了良好效果，也证明HSMM模型比HMM模型能更好地描述耐火砖的退化过程，更适合对耐火砖进行剩余寿命预测。